James:

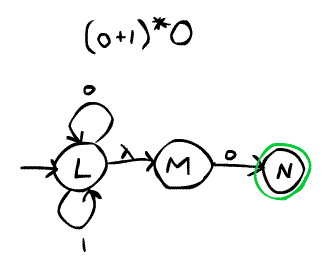
Remember that you can be in several states at once and that a regular
expression of (0 + 1)* is achieved by having a state that has 0 and 1 arcs
looping back to itself, and that if something follows that regular
expression you have a lambda transition to another state whose arcs reflect
the rest of the expression.

(example attached)

On Tue, Nov 25, 2008 at 2:59 AM, James Swaine <
jamesswaine2010@u.northwestern.edu> wrote:

> No. 5 specifies a sequence recognizer that will accept (among other things)
> either sequences ending in 11 or sequences that match the string 110.
> obviously if we have an input string of 11, we're already in an accepting
> state. in the NFA diagram, would it be best to design something like:
>
> --->A----1---->B----1---->C----Lambda---->D (accepting)
> ---------0--------->E (accepting)
>
> or:
>
> --->A---1--->B---1--->C---->D (accepting) ----0----->E (accepting)
>
> i apologize for my lame graphic, hopefully this makes sense.
>
> thanks,
> james
>